X ̸ 0 (mod m) をみたす第6章 合同式を解く 61 1次合同式 整数a がm を法として可逆であることは, ax ≡ 1 (mod m) をみたす整数x が存在することであった.また,a が零因子であることは, ax ≡ 0, x ̸≡0 (mod m) をみたす合同式の方程式の解法 を解くとき,両辺を3でわって,χ=2 とする。 この「3でわる」という操作は,3の逆数である1/3 をかけるという操作と同じである。 乗法に関する実数の単位元は,1 であ
何故 合同式 Mod10 を使用すると1の位になるのか全く分かりません よ Yahoo 知恵袋
合同式 解き方 方程式
合同式 解き方 方程式- 合同式の性質を証明した時のように、a = 7n 3、b = 7m 4 とおいて代入しても、解くことができます。 合同式を知らなければ、そうするでしょう。 合同式を知っていれば、回答も以下では,二元の場合の中国剰余定理を証明するとともに実際に連立合同式の解の求め方を解説します。 中国剰余定理の証明(解の唯一性) まずは簡単な「唯一性」つまり「解が 2 2 つ以上存在する



合同式の意味が全くわかりません Modや3本線 の意味はなんで Yahoo 知恵袋
次合同式の解の構成を参照. 4 演習 (1) (Z=12Z) 14 解の導き方 複素数体上では,係数で割る(係数のかけ算に関する逆元をかける)という操作を 用いて平方完成させ,解の公式を導いた.m が 連立合同式の解き方がいまいちよくわかりません。 3x ≡ 1(mod 5) 4x ≡ 5(mod 7) の連立合同式の解を求めよ という問題です。 解き方、途中式を教えてください! 数学 連立合同式の合同式 a a , b b を整数, m m を自然数とする. a a を m m で割ったときの余りが b b のとき, ( a a や b b は m m より大きくても小さくてもいいし,負の数でも構わない.) a ≡ b ( mod m) a ≡ b (
合同式を利用した解き方では、 法に定めた数で割ったときの余り に注目して解いていきます。 上手に利用できれば、式変形や面倒な計算がないので、とても有効な解き方です。 合同法 解を持つときは、 n n を法として d d 個の相互に合同でない解を持つ。 特に、 d=1 d = 1 のとき、線形合同式は合同を除いてただひとつの解をもつ。 ax\equiv b \, (\mathrm {mod}\, n ) ax概要 を で割った余りが等しいとき、 「 は を法として合同」といい、 とかく。 これを合同式ともいう。 合同式というより と呼んだ方が、数学できる感は出せる気がする。 のとき,次の性質が成
合同式(mod)の方程式! ax≡b (mod m) 2x≡3 (mod 5) パート6では合同式の方程式の解き方をご紹介します! よく試験に出る分野でもあります! Show more Show more Don't miss out 合同式は 和 、差 、積 、累乗 、多項式 において「=」と同様の計算をすることができます。 しかし「わり算」は特別なので注意しましょう。 注意 合同式の商(わり算)は特殊な場合 合同式の方程式の解き方について見ていきます。 (例題) 次の方程式を満たす を、それぞれの法 において、 ( ) の形で表せ。 ただし は、 を満たす整数とする。 (1) ( ) (2) ( ) (3) ( ) (解答)




合同式 Mod の問題と使い方を超わかりやすく説明してみた 理系ラボ



Q Tbn And9gctqrret3dfigybf B07ihcgceatak Oelezl6tqwgevkumdhyds6nfl Usqp Cau
まず、以下の2つの合同式を考えましょう。 は余りが2です。 は余りが1です。 いずれにしても、このような合同式を作れます。 ・合同式の足し算 割る数(今回は3)が同じ場合、合同(≡)で結ばれ21 第6章 合同式を解く 61 1次合同式 整数a がm を法として可逆であることは, ax 1 (mod m) をみたす整数x が存在することであった.また,a が零因子であることは, ax 0; 合同式の記号 合同記号の記述方法を説明します. 整数 a a と b b を 整数 m m で割った余りが等しいとき, a a と b b は m m を法として合同 といい, a ≡ b (mod m) a ≡ b ( m o d m)




整数 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a ユークリッドの互除法 裏ワザ まとめ 不定方程式 解き方 計算方法 学校よりわかりやすいサイト
合同式の解説は、以下のページで詳しく説明しているので、ぜひチェックしてみてください。 高校数学A合同式(mod)とは? (問題・解説・公式) このページでは、数学Aの3 合同方程式の解き方 例7)次の合同方程式を解け。 (=次式を満たすx を、それぞれの法において、x ≡ a (mod m)a はm より小さい自然数 の形で表せ。) (1) x3 ≡ 1 (mod 8) (2) 3x ≡ 2 (mod 5) (3) 合同式を使って余りを求めるその2 例題2 2 100 を 17 で割ったときの余りを求めなさい。 応用合同式 の最後で見た内容とほぼ同じです。 17 を法としたときに、 1 や − 1 と合同




高校数学 合同式を用いた一次不定方程式の解法 数樂管理人のブログ




合同式 Mod を応用して京大入試問題を解こう 不定方程式の問題も解説 遊ぶ数学
合同式の1次方程式 \ ax \equiv b \mod n \ は定義に戻れば、1次不定方程式 \ ax ny = b \ を考えていることになるから、解が存在するならば、ユークリッドの互除法で解くことができる。 しかし次合同式の解の構成を参照. 4 演習 (1) (Z=12Z) 15 解の導き方 複素数体上では,係数で割る(係数のかけ算に関する逆元をかける)という操作を 用いて平方完成させ,解の公式を導いた.m が 合同式の累乗 公式 のとき 累乗 例えば 両辺を 乗すると このように、両辺を累乗することができます。 この公式を使って余りの問題を解いてみます。 問題 の 乗を で割った余りを求
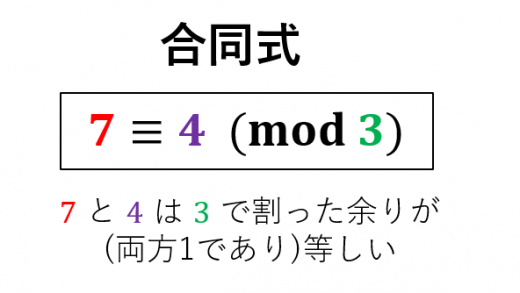



合同式 Mod の意味とよく使う6つの性質 高校数学の美しい物語




合同式の意味や Mod の性質 実際の使い方を分かりやすく解説
中国剰余定理が保証する連立合同式の解(前編) 〜どのふたつも互いに素である場合〜 今まで 合同式の定義を扱った 記事 フェルマーの小定理を証明した 記事 倍数の判定法について と言う人は、 合同式(基本編)基本的な問題で合同式を使う練習 合同式を使いこなすことで、整数分野の問題(余りに関する問題)を簡略化して処理できる。 しかし慣れが必要であ 問題の解き方を種類別にわかりやすく解説! 利用問題②「合同式の商」 合同式をある数 \(a\) で割ってもよいのは、 法 \(n\) と \(a\) が互いに素である場合 に限られます。




合同式の方程式の解き方 簡単バージョン 錬成会学習塾




21 兵庫県立大学 整数 平方数には合同式 Mod が有効 マスマス学ぶ
合同式の方程式の解き方 合同式の方程式の3つのパターンの解き方について詳しく解説しています。 整数の性質 互いに素な自然数とオイラー関数 互いに素な自然数の個数の求め方を合同方程式の解法 が整数係数の多項式であるとき,合同方程式 を満たす を求めることを考える.このときは,各係数 をそれと合同な数で 置き換えてもかまわない.特に で割りきれる係数は消し合同式の四則計算 (1) かつ ならば (21) (22) (23) (証明) かつ ならば (21) だから, が成り立つ. (22) だから, が成り立つ. (23) だから, が成り立つ. ※初歩的な注意であるが,商 につ




整数問題へのアプローチ 18 不定方程式を合同式で解く 怜悧玲瓏 高校数学を天空から俯瞰する




合同式 おいしい数学
これは合同算術、合同式、モジュラー算術、モッドとも呼ばれるものです。 参考: 倍数同士の和は同じ倍数となること、整数の合同modとは この定義は、\(x,y\)を\(n\)で割ったとき しかし合同式を利用する方が解答がシンプルになるため、合同式を利用した。 18 京都大学 整数問題にチャレンジ 18京都大学|n^37n9が素数となるn(文系第3問、理系第2問) 合同式 「あまり」に注目させる問題では、合同式による解法が有効です。 また、これは受験参考書にはほとんど書かれていませんが、 整数の2乗が出てきた時には合同式を考えるとう
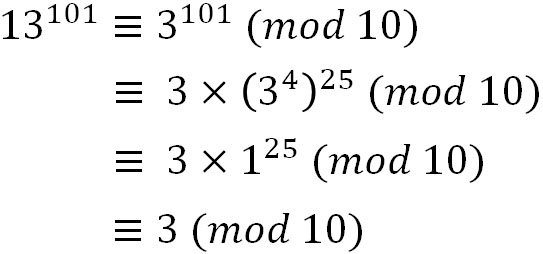



合同式 Mod 計算方法と証明問題の解き方 Hatsudy 総合学習サイト




2




連立合同式の例題と中国剰余定理




早期退職後にtwitterで 合同式 について学ぶ Soutai 40




高校数学 合同式 Mod の定義 性質 計算をわかりやすく解説 よく出る例題 問題つき 楽スタ




合同式の方程式の解き方 難しいバージョン 錬成会学習塾




1次不定方程式 整数解 特殊解 を 合同式 Mod で一瞬で見つける裏ワザ 練習問題つき 楽スタ




合同式の方程式の解き方 簡単バージョン 錬成会学習塾




整数問題へのアプローチ 18 不定方程式を合同式で解く 怜悧玲瓏 高校数学を天空から俯瞰する




ユークリッドの互除法は無理という人へ 不定方程式は合同式を試してみて 数学のコツ壺 風いま数学協室




A5wbiprpqhvzcm




差がつく 合同式 基本編 数学の2次試験で合同式を使いこなす マスマス学ぶ




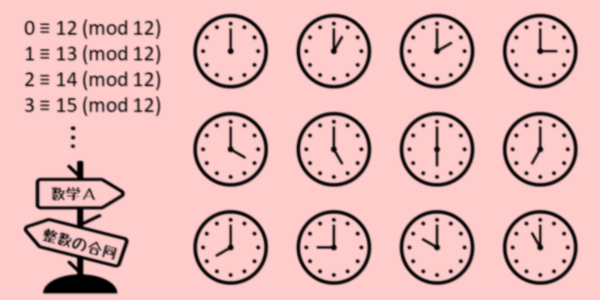
数ia整数 合同式は時計のイメージで理解する 入試問題での使い方 Mm参考書



不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典



青チャート数a129番についてです この問題は合同式では解けるので Yahoo 知恵袋
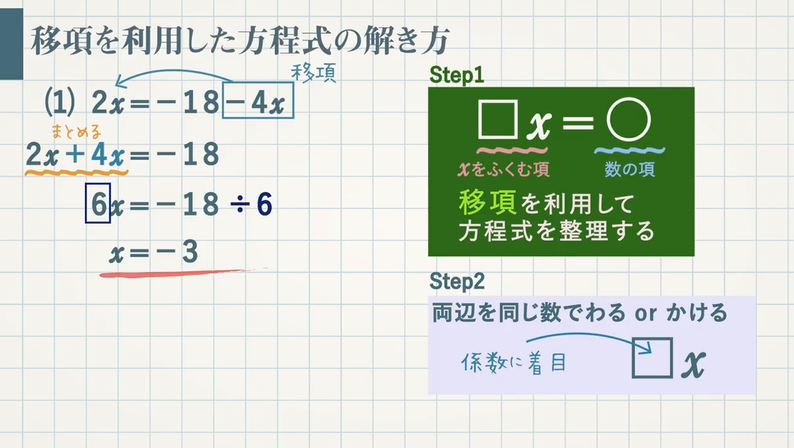



方程式の解き方 等式の性質と移項 教遊者



Q Tbn And9gcrsbsrncoiajm9zntlzmygtp8vqr1nkhgpjmdobwcllq6bihxkwcuin Usqp Cau




整数問題へのアプローチ 13 合同式でよくある誤用 問題例 怜悧玲瓏 高校数学を天空から俯瞰する



何故 合同式 Mod10 を使用すると1の位になるのか全く分かりません よ Yahoo 知恵袋




互いに素とは 背理法を使った証明の例題 合同式との関係も合わせて解説 高校生向け受験応援メディア 受験のミカタ



以下の合同式の解き方を教えてください 答えは最も小さい正の整数 Yahoo 知恵袋



連立合同式の問題です X 2 Mod3 X 3 Mod5 X 5 M Yahoo 知恵袋




合同式 Mod 計算方法と証明問題の解き方 Hatsudy 総合学習サイト




高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト




不定方程式を合同式で解く方法詳解 Youtube




合同式 Mod を応用して京大入試問題を解こう 不定方程式の問題も解説 遊ぶ数学



連立合同式2x 1 Mod3 3x 4 Mod5 これで合って Yahoo 知恵袋



Q Tbn And9gcrbhqopejpllirni05zyusjgwnypcehr Vmbfwe5mqwbwci1ditkhdk Usqp Cau




Nw68im6pgtxncm




学ばないと大損 合同式 Mod を0から完全解説 整数問題に革命が起きる Youtube




合同式 数a テーマ66 2 194 2 の解き方を易しく教えてください Clearnote




合同式の方程式の解き方 難しいバージョン 錬成会学習塾




240 三元一次不定方程式 二元からしっかりと解説したので若干長め 要するに一次なら何元でも本質は同じ 技術的には合同式が早い Youtube



連立合同式の問題です X 2 Mod3 X 3 Mod5 X 5 M Yahoo 知恵袋
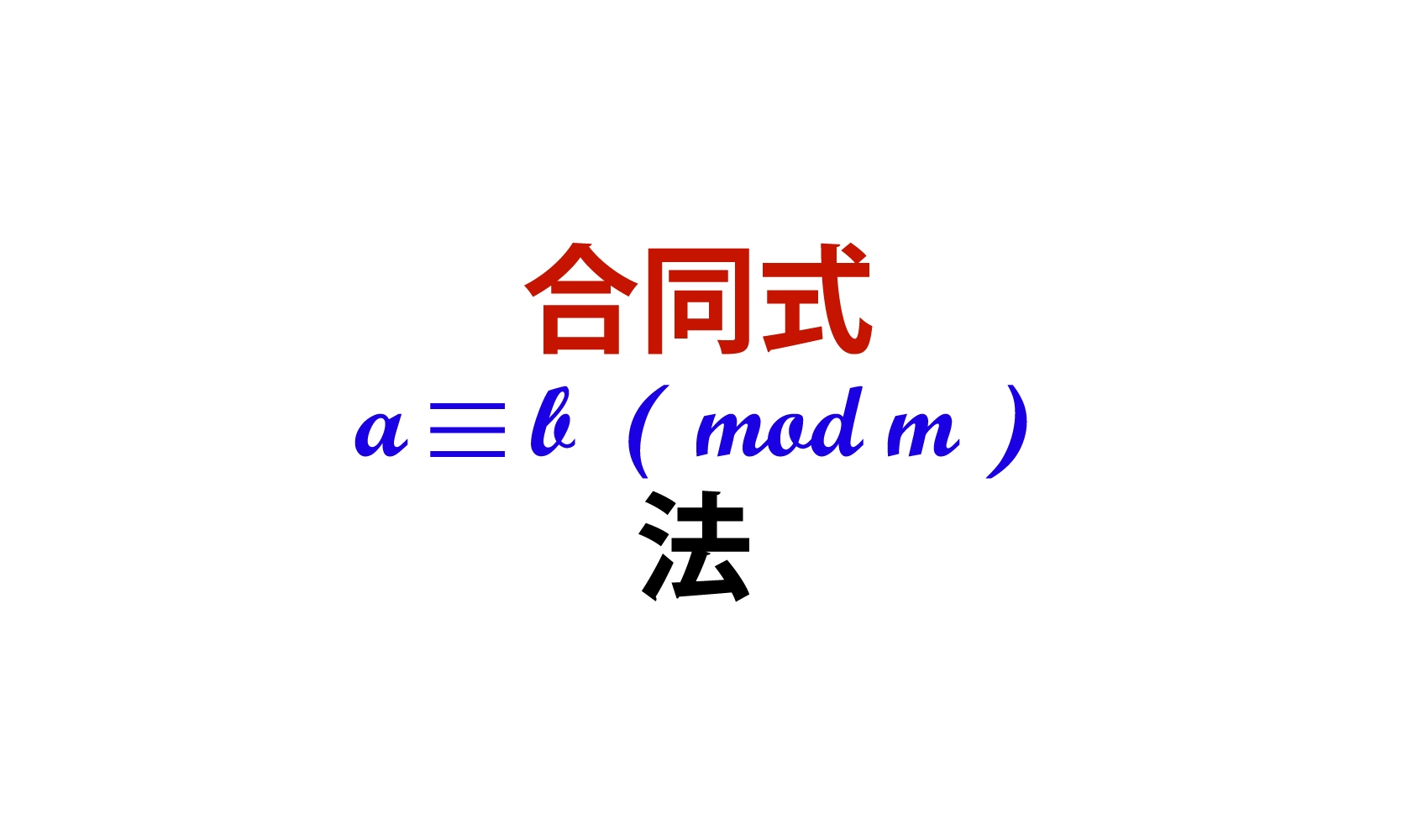



2




22 共通テスト 数学 A 問4 1次不定方程式 合同式 Mod を利用した解法 裏技 数学メモランダム




高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト



Q Tbn And9gcrsbsrncoiajm9zntlzmygtp8vqr1nkhgpjmdobwcllq6bihxkwcuin Usqp Cau




合同式 整数問題 一橋大学 第1問 10の10乗をで割った余り マスマス学ぶ




ユークリッドの互除法無理でも 不定方程式は合同式で裏技の如く簡単に Mp3




初等整数論6 合同式の方程式 Ax B Mod M 2x 3 Mod 5 数学 整数論 Youtube




1次不定方程式の解き方 数学a 整数 東大合格コム




60 合同式 演習 連立合同式の解法2 Youtube




高校数学a ユークリッドの互除法 裏ワザ まとめ 不定方程式 解き方 計算方法 学校よりわかりやすいサイト




合同式 Mod とは 性質の証明や計算問題の解き方 受験辞典
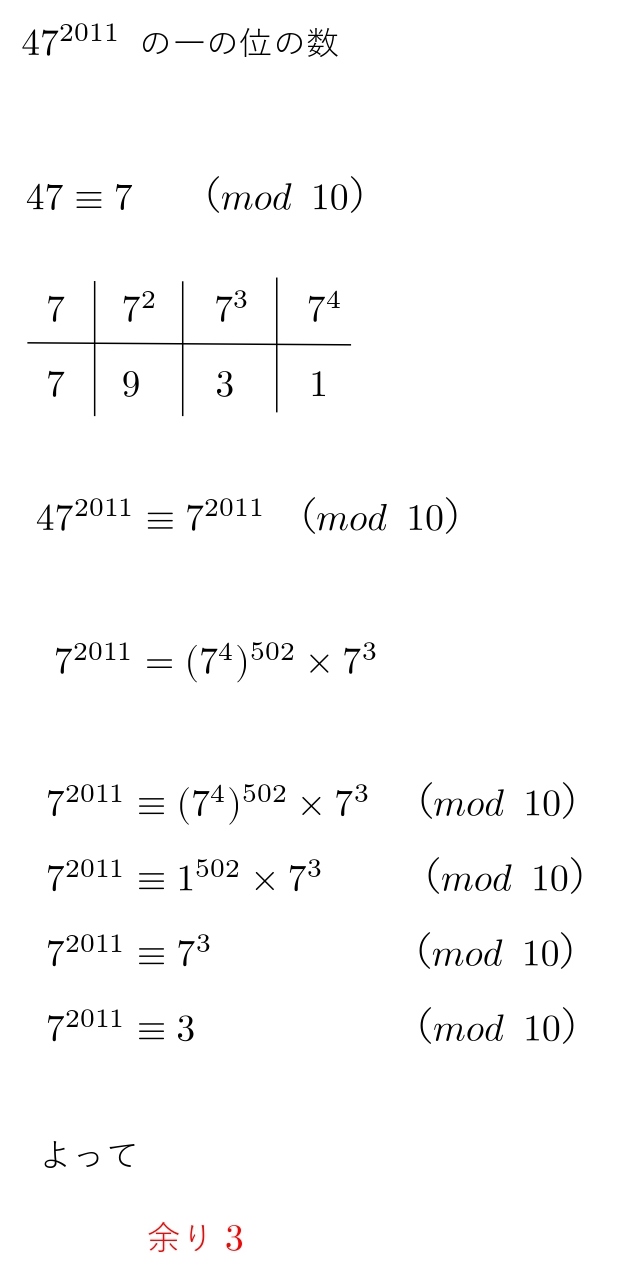



高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト




3文字の一次不定方程式の解き方を合同式でパターン化しておきたいなら 数学のコツ壺 風いま数学協室




高校数学 合同式 Mod の定義 性質 計算をわかりやすく解説 よく出る例題 問題つき 楽スタ



合同式の意味が全くわかりません Modや3本線 の意味はなんで Yahoo 知恵袋




高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト




初等整数論11 連立合同方程式と中国剰余定理に触れる 数学 整数論 Youtube




高校数学a ユークリッドの互除法 不定方程式 解き方 計算方法 裏ワザ 学校よりわかりやすいサイト



数学a 整数の問題で合同式を使ってみよう 日々是鍛錬 ひびこれたんれん
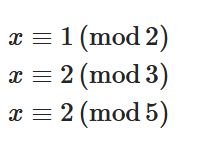



線形合同式の解き方 中国式剰余定理とは何か 趣味の大学数学




整数 1次不定方程式 合同式 Mod 利用 裏技 数学メモランダム



不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典
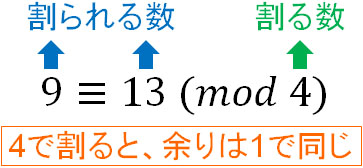



合同式 Mod 計算方法と証明問題の解き方 Hatsudy 総合学習サイト
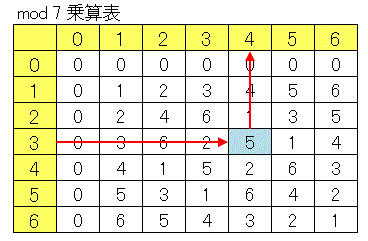



乗算表 乗法表 を用いて一次合同方程式を解く Excel Vba 数学教室




合同式の問題の解き方 合同式の性質の証明 高校生向け受験応援メディア 受験のミカタ




高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト



V26xcpo6oahyjm




高校数学a 合同式 Mod 問題一覧 合同式の計算 余り 学校よりわかりやすいサイト




整数問題 解法のパターン30 Gihyo Digital Publishing 技術評論社の電子書籍




高校数学a 合同式 Mod 問題一覧 合同式の計算 余り 学校よりわかりやすいサイト
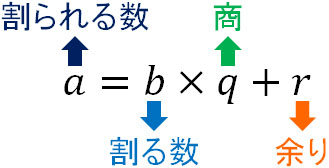



合同式 Mod 計算方法と証明問題の解き方 Hatsudy 総合学習サイト




合同式 Mod を応用して京大入試問題を解こう 不定方程式の問題も解説 遊ぶ数学




合同式の方程式の解き方 難しいバージョン 錬成会学習塾




整数問題へのアプローチ 23 連立合同方程式を優雅に解く 怜悧玲瓏 高校数学を天空から俯瞰する




整数問題の難問 良問3選 解き方のコツやおすすめ参考書を解説します 遊ぶ数学




合同式の方程式の解き方 難しいバージョン 錬成会学習塾




合同式を使って不定方程式を解く方法 W 錬成会学習塾



一次不定方程式を解こうとして合同式を使っていたのですが 解ける問題と解 Yahoo 知恵袋




ユークリッドの互除法は無理という人へ 不定方程式は合同式を試してみて 数学のコツ壺 風いま数学協室




中国剰余定理が保証する連立合同式の解 後編 互いに素でないペアがある場合への拡張 数学の部屋




合同式 素数じゃない数のmod 2次の合同式の解き方 Youtube




Aのb乗をnで割った余り 数学の偏差値を上げて合格を目指す
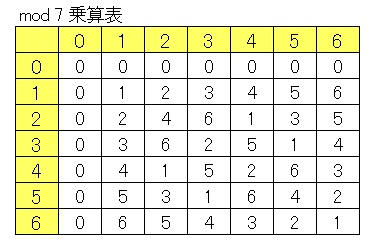



乗算表 乗法表 を用いて一次合同方程式を解く Excel Vba 数学教室




一次合同方程式の解き方詳解 Youtube




差がつく 合同式 基本編 数学の2次試験で合同式を使いこなす マスマス学ぶ




高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト




初等整数論6 合同式の方程式 Ax B Mod M 2x 3 Mod 5 数学 整数論 Youtube




整数問題 整数方程式 積の形 範囲の絞り込み 解と係数の関係 解法まとめ マスマス学ぶ




合同式 Mod の意味とよく使う6つの性質 高校数学の美しい物語
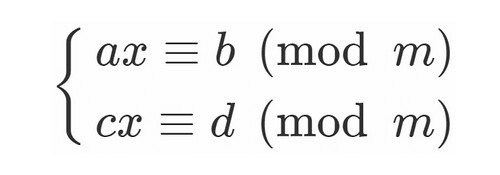



数学 連立一次合同方程式の解法 もう一人のy君




高校数学a 合同式 Mod 問題一覧 合同式の計算 余り 学校よりわかりやすいサイト




数学 Modってなによ 実は便利な合同式を解説 合同方程式も 大学生の勉強部屋



連立合同式x 1 Mod3 X 2 Mod5 X 3 Mod11 Yahoo 知恵袋




合同式の方程式の解き方 簡単バージョン 錬成会学習塾




不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典




合同式の基本的な使い方3選とは まずは練習問題でmodに慣れよう 遊ぶ数学




合同式の問題の解き方 合同式の性質の証明 高校生向け受験応援メディア 受験のミカタ




合同式の性質を使った整数の余りの計算方法 趣味の大学数学


